Aula 007

Frequência

Numa pesquisa, muitas vezes temos uma variável quantitativa. Então, ao colhermos os dados, nos deparamos com uma lista de valores numéricos.

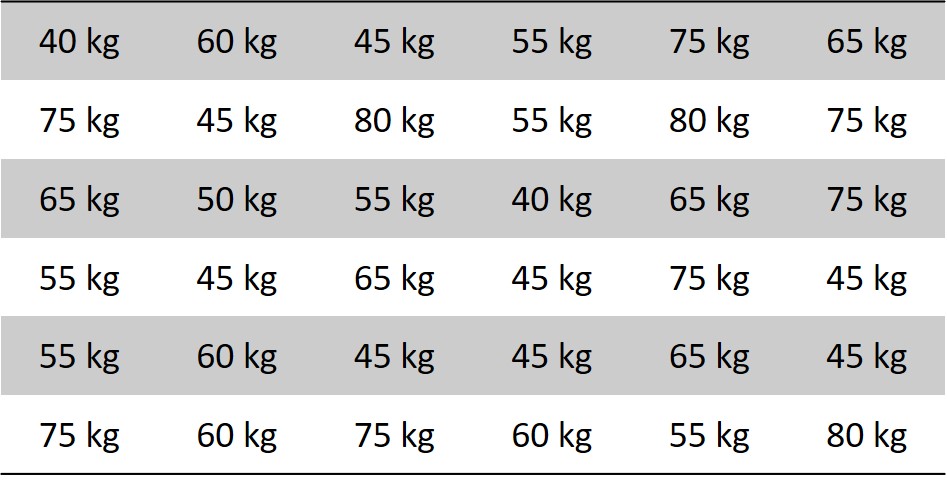
Uma das coisas que podemos fazer com essa lista é verificar a frequência de cada elemento. Para isso, o primeiro passo é organizar esses dados em ROL, crescente ou decrescente, de acordo com a preferência do pesquisador.

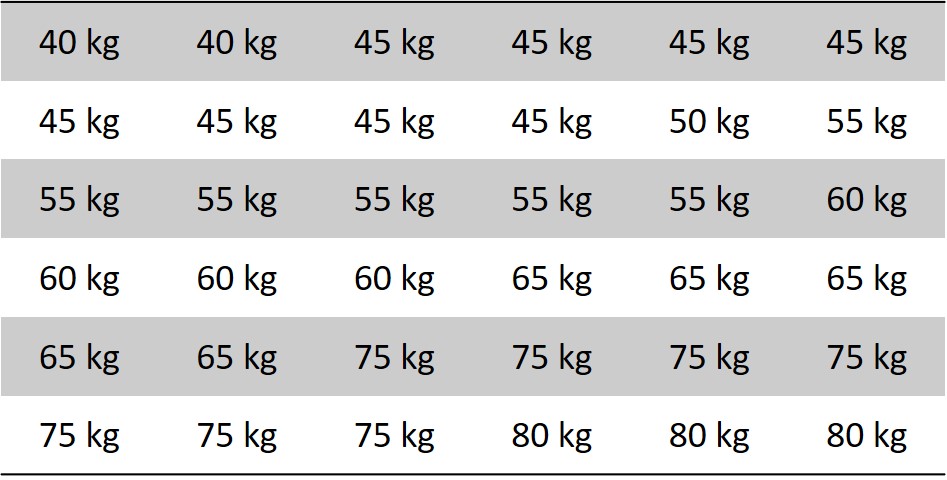
A partir desse ROL, podemos organizar os dados em uma tabela de frequência. Para isso, basta contar a quantidade de vezes que cada elemento aparece.

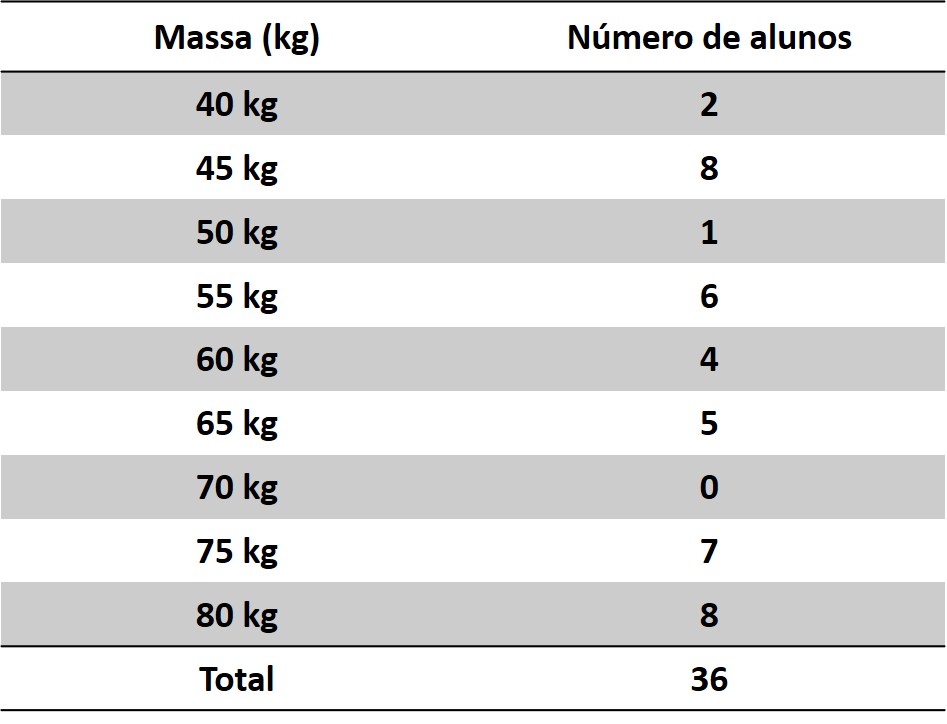
Mas o que é frequência?

Frequência é a quantidade de vezes que um dado surge no conjunto de dados.

Tipos de frequência

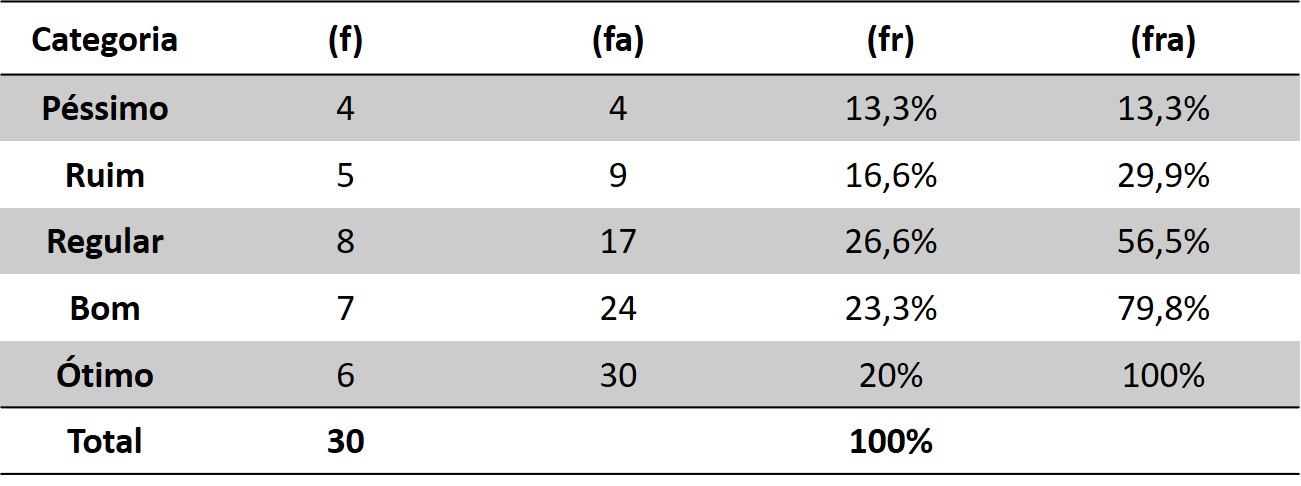
Na estatística, o estudo sobre frequências se subdivide em dois grupos que se diferenciam de acordo com a sua função na tabela:

• Frequência absoluta (f)
  • A frequência absoluta representa a quantidade exata de vezes em que cada elemento (ou classe) apareceu na coleta.
• Frequência relativa (fr)
  • A frequência relativa compara cada categoria com o todo, sendo representada na forma de decimal ou em porcentagem.

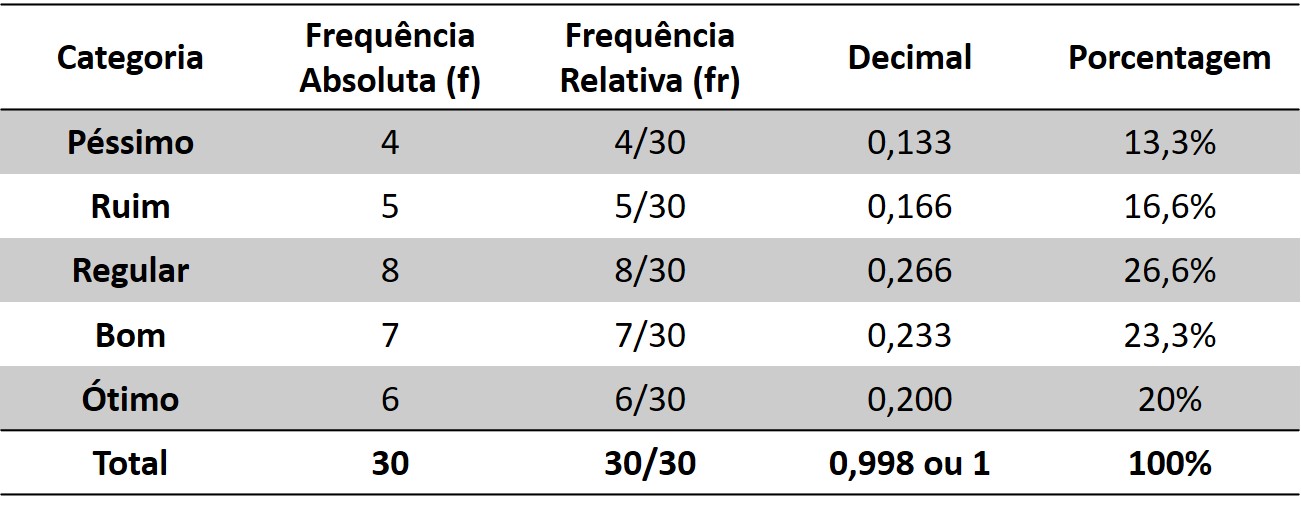
• Frequência absoluta acumulada (fa) e frequência relativa acumulada (fra)
  • Nessas frequências, a contagem de cada categoria vai sendo acumulada nas demais.

Intervalos

Às vezes, principalmente quando lidamos com variáveis quantitativas contínuas, acabamos com um rol com muitas categorias. Nesses casos, organizar uma tabela de frequência se torna inviável. Imagine, por exemplo, ter notas de 70 alunos, sendo que cada aluno pode ter uma nota diferente?

Para resolver esse problema, dividir os dados em intervalos de classes e usar esses intervalos como categorias.

Vejamos o exemplo abaixo.

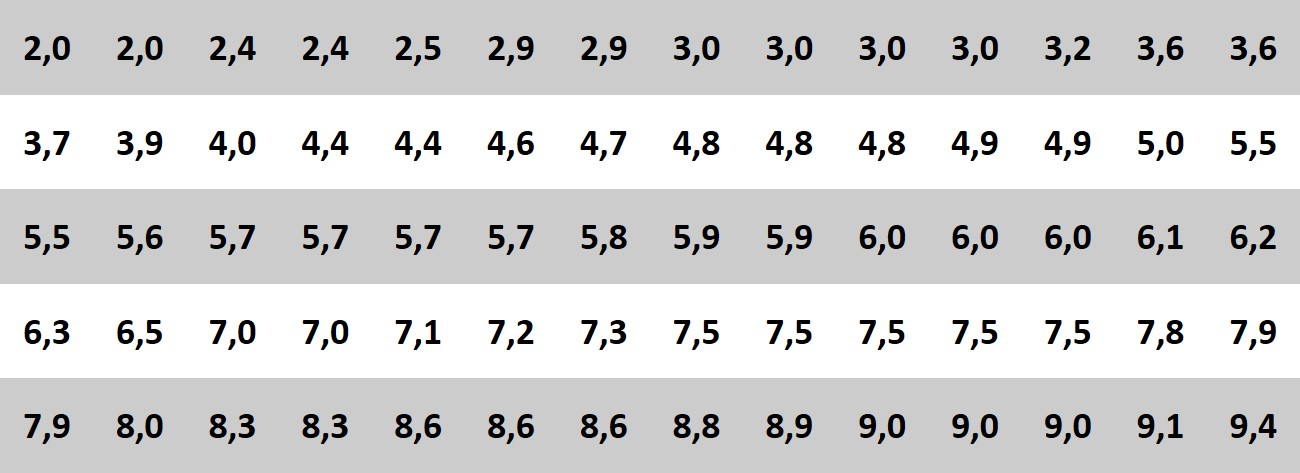
Se fossemos montar a tabela de frequêcia desse ROL, sem o uso de intervalos, teríamos o seguinte resultado:

Como podemos ver, a tabela acima é tão longa que foi necessário dividí-la em duas para que fosse possível visualizá-la. Se tivéssemos mais categorias, a tabela seria ainda maior.

Para evitar esse tipo de situação e facilitar a compreensão e manipulação dos dados, agrupamos as categorias em intervalos.

O intervalo de classe representa um espaço delimitado por dois valores, incluindo eles ou não, cuja frequência será dada pela a quantidade de elementos que fazem parte desse grupo.

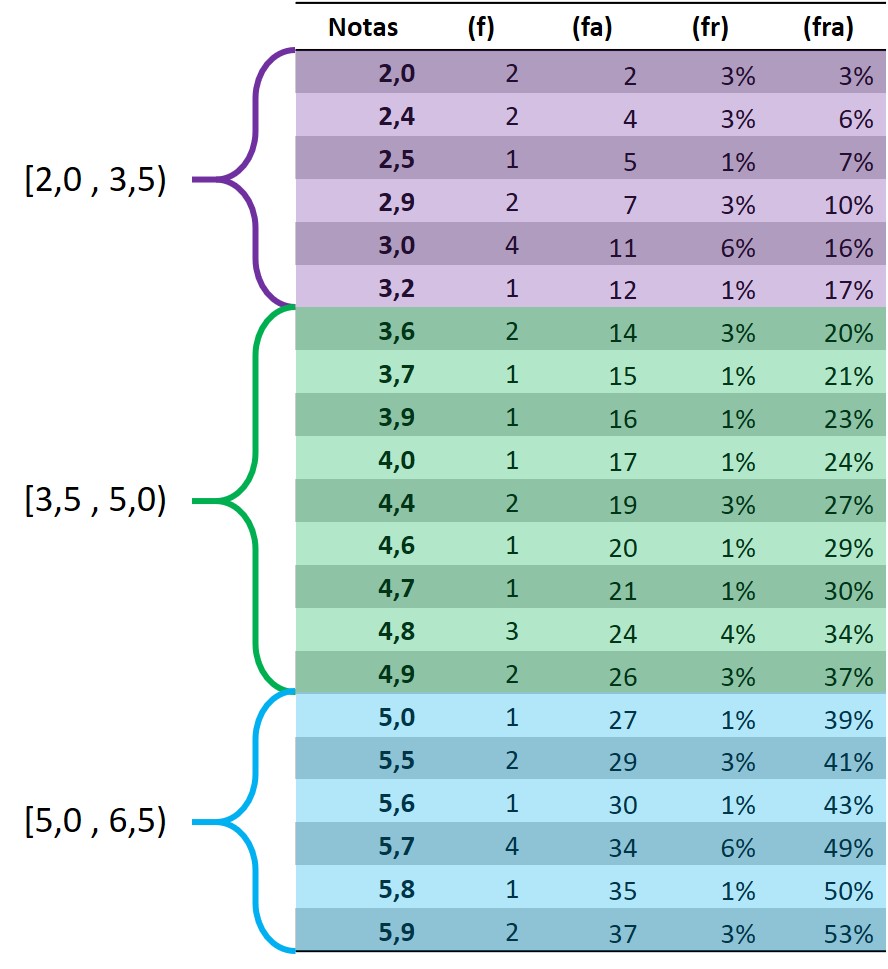
No exemplo acima, temos um intervalo entre e 2,0 e 3,5, não incluindo o 3,5. Esse intervalo é representado por \([2,0 \medspace,\medspace 3,5)\). Neste intervalo, existem 12 elementos. No intervalo seguinte, \([3,5 \medspace,\medspace 5,0)\), temos 14 elementos.

Cabe notar também, nesse exemplo, que a amplitude (tamanho do intervalo ou diferença entre o maior e menor valor) é igual a 1,5.

Assim, temos a seguinte tabela de frequência:

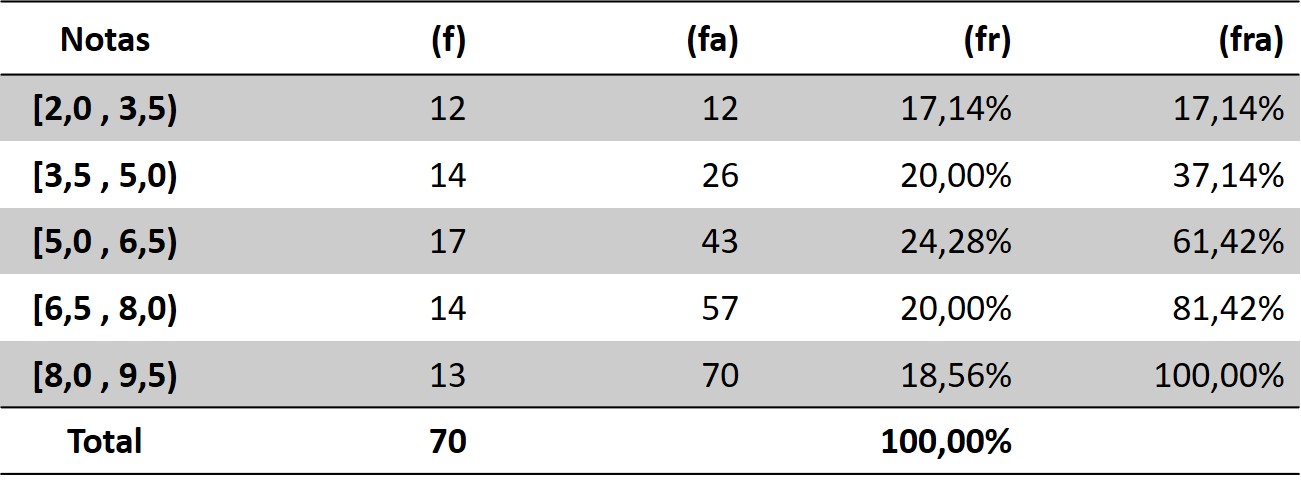
Neste caso, a amplitide foi definida pesquisador a partir de critérios subjetivos. Porém, existem orientações para se definir o tamanho ideal de uma classe.

As mais utilizadas são:

• Regra de Sturges - Regra do Logaritmo
  • \[k = 1 + 3,3 \log (n)\]
• Regra da potência de 2 - Regra da Desigualdade
  • \[k = \text{menor valor inteiro tal que } {2^k} \ge n\]
• Regra da Raiz Quadrada
  • \[k = \sqrt{n}\]

Onde:

• k = número de classes
• n = número total de observações na amostra

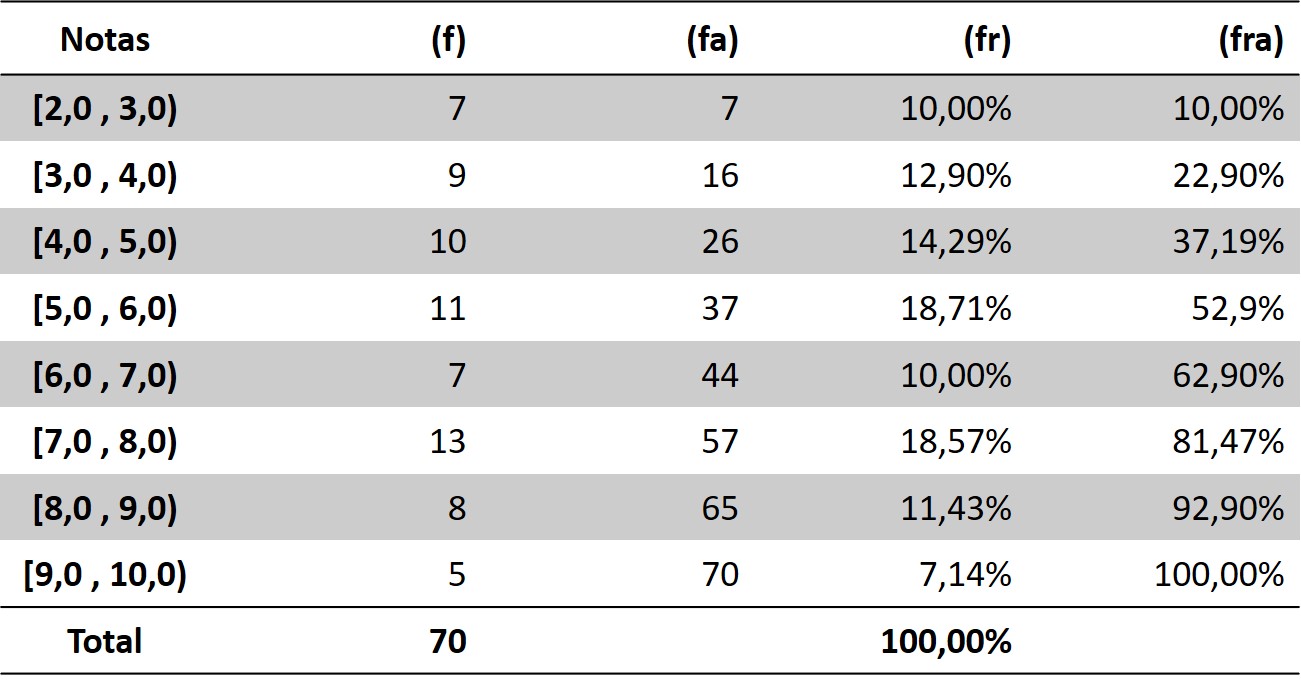
Para o caso acima, usando o critério da Raiz Quadrada, temos:

\[k = \sqrt{70}\] \[k = 8,36\]

Ou seja, aproximadamente 8 classes. Dessa forma, para calcular a amplitude, temos:

\[(9,4 - 2,0) / 8 = 0,92\]

Arredondando, temos uma amplitude de 1. Dessa forma, temos a seguinte tabela de frequência:

Exercícios

Exercício 1

Os dadosque seguem representam as idades, em anos, completos, de todas as crianças atendidas em certo dia por um posto de puericultura. Organize os dados e construa a tabela de frequência com as seguintes frequências: absoluta, relativa e as respectivas frequencias acumuladas.

1	3	0	1	1	8	2	3	1
1	2	5	0	3	4	1	2	0

Exercício 2

De uma análise de dados de balanço de 49 indústrias, obtiveram-se os valores seguintes para seus coeficientes de liquidez. Organize os dados, agrupe-os em classe com base no critério de raiz quadrada e construa uma tabela de frequência com as seguintes frequências: absoluta, relativa e as respectivas frequências acumuladas.

3,5	2,3	5,4	5,5	16,7	8,7	9,1
14,6	7,3	11,4	7,9	15,8	2,8	18,9
11,9	16,2	7,0	5,3	2,7	7,4	16,1
13,3	18,7	5,7	8,7	9,0	10,5	12,2
19,4	0,9	3,1	9,6	5,8	1,6	7,0
8,5	2,7	10,6	15,5	0,5	12,7	13,5
16,7	19,1	11,9	4,8	14,9	6,9	1,8

Exercício 3

EEAR 2019/1 - A tabela apresenta as frequências acumuladas das notas de 70 alunos, obtidas em uma avaliação. A frequência absoluta da 2ª classe é:

• a) 14
• b) 15
• c) 16
• d) 17

Notas	Frequência Acumulada
[2,0 , 3,5)	12
[3,5 , 5,0)	26
[5,0 , 6,5)	43
[6,5 , 8,0)	57
[8,0 , 9,5)	70

Resolução dos exercícios

Resolução do Exercício 1

Passo 1: Primeiro, organizamos os dados acima em rol.

0

0

0

1

1

1

1

1

1

2

2

2

3

3

3

4

5

8

Passo 2: Montamos a tabela de frequências.

Idade	(f)	(fa)	(fr)	(fra)
0	3	3	16,7%	16,7%
1	6	9	33,4%	50,1%
2	3	12	16,7%	66,8%
3	3	15	16,7%	83,5%
4	1	16	5,5%	89,0%
5	1	17	5,5%	94,5%
8	1	18	5,5%	100,0%
Total	18		100,0%

Resolução do Exercício 2

Passo 1: Organizar os dados em rol:

0,5	0,9	1,6	1,8	2,3	2,7	2,7
2,8	3,1	3,5	4,8	5,3	5,4	5,5
5,7	5,8	6,9	7,0	7,0	7,3	7,4
7,9	8,5	8,7	8,7	9,0	9,1	9,6
10,5	10,6	11,4	11,9	11,9	12,2	12,7
13,3	13,5	14,6	14,9	15,5	15,8	16,1
16,2	16,7	16,7	18,7	18,9	19,1	19,4

Passo 2: Calcule o número de classes, usando o critério da raiz quadrada:

\[n = 49\] \[k = \sqrt{n}\] \[k = \sqrt{49}\] \[k = 7\]

Passo 3: Calcule a amplitude de cada classe:

\[amplitude = (19,4 - 0,5) / 7\] \[amplitude = (18,9) / 7\] \[amplitude = 2,7\]

Passo 4: construa a tabela de frequência

Idade	(f)	(fa)	(fr)	(fra)
[0,5 , 3,2)	9	9	18%	18%
[3,2 , 5,9)	7	16	14%	33%
[5,9 , 8,6)	7	23	14%	47%
[8,6 , 11,3)	7	30	14%	61%
[11,3 , 14)	7	37	14%	76%
[14 , 16,7)	6	43	12%	88%
[16,7 , 19,5)	6	49	12%	100%
Total	49		100%

Resolução do Exercício 3

Passo 1:

Para saber a frequência absoluta da segunda classe, basta subtrair a frequência acumulada da primeira da frequência acumulada da segunda.

\[(f) = 26 - 12\] \[(f) = 14\]

Resposta: a) 14