Aula 08

Para calcular a probabilidade de um evento complexo, nós decompomos esse evento em em eventos elementares e calculamos as probabilidades desses eventos elementares. Então, aplicando os teoremas de Probabilidade, a partir das probabilidades elementares, nós usamos as operações com eventos para calcular a probabilidade do evento complexo.

Cada uma das operações com eventos tem a sua correspondência num Teorema da Probabilidade.

Teorema do Evento complementar

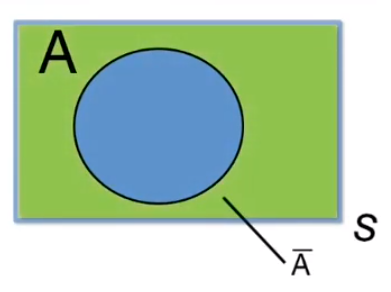
O evento complementar é a não ocorrência do evento.

A probabilidade da ocorrência do evento complementar é 1 menos a probabilidade do evento considerado.

\[P(\bar A) = 1 - P(A)\]

Exemplo: Se a probabilidade de um aluno não passar de ano é \(P(A) = 0,7\), então a probabilidade dele não passar será \(P(\bar A) = 1 - 0,7 = 0,3\).

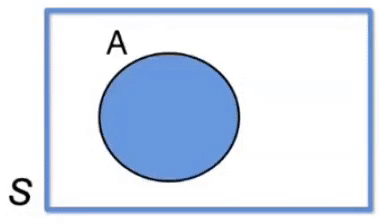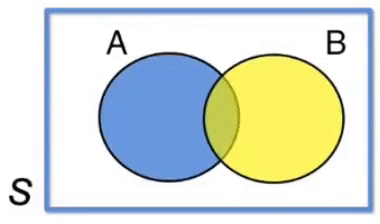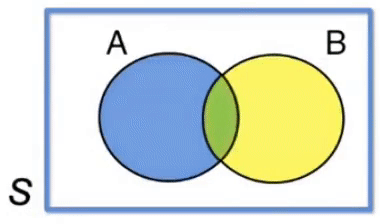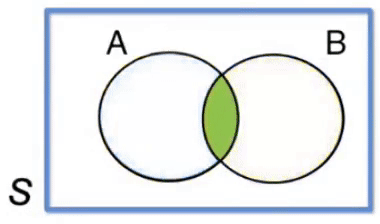
Teorema da União

\[P (A \cup B) = P(A) + P(B) - P(A \cap B)\]

Se os eventos \(A\) e \(B\) forem mutualmente excludentes, ao cálculo do evento união, é feito simplesmente pela soma das probabilidade dos eventos. Ou seja:

Se \(P(A \cap B) = 0,\) então \(P(A \cup B) = P(A) + P(B)\)

Para o caso de 3 eventos, temos:

\[P (A \cup B \cup C) = P(A) + P(B) +P(C) - P(A \cap B) - P(A \cap C) - P(B \cap C) + P(A \cap B \cap C)\]

Probabilidade condicionada

Probabilidade condicionada é um segundo evento de um espaço amostral que ocorre em um evento depois que já tenha ocorrido o primeiro.

Para melhor compreensão do que seja probabilidade condicional, considere um espaço amostral \(S\) finito não vazio e um evento \(A\) de \(S\).

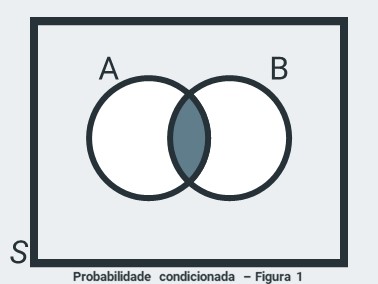
Se quisermos outro evento \(B\) desse espaço amostral \(S\), essa nova probabilidade é indicada por \(P(B \vert A)\) e dizemos que é a probabilidade condicional de \(B\) em relação a \(A\).

Essa probabilidade condicional irá formar um novo espaço amostral, pois agora o espaço amostral será \(A\) e os elementos do evento \(B\) irão pertencer a \(B \cap A\).

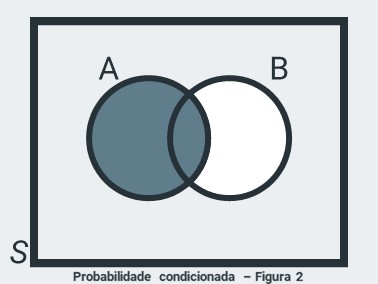
Para calcular a probabilidade \(P(B \vert A)\) deve-se seguir o mesmo raciocínio da fórmula \(P(A) = \frac{n(A)}{n(S)}\) portanto:

\(P(B \vert A) = \frac{n(B \cap A)}{n(A)}\) ou \(P(B \vert A) = \frac{P(B \cap A)}{P(A)}\)

Exemplo:

Ao tirar uma carta de um baralho de 52 cartas, qual a probabilidade de sair um Rei de Ouros?

Segundo a definição clássica, a probabilidade é \(P(A) = \frac{1}{52}\)

Agora vamos realizar novamente a experiência. Embaralhamos o baralho e tiramos 1 carta. Antes de saber qual a carta, algúem lhe dá uma informação: essa carta é uma figura. Qual a probabilidade de sair novamente um Rei de Ouros?

Um baralho tem 4 naipes (ouros, paus, espada e coração) e cada naipe tem 3 figuras (J, Q e K), logo um baralho de 52 cartas tem 12 figuras.

Dessa forma, a probabilidade \(P(A) = \frac{1}{12}\).

Pelo caso acima podemos concluir que o papel da nova informação é reduzir o espaço amostral, restringindo o número de possibilidades, criando um espaço amostral diferente.

Teorema da Intersecção ou Teorema do Produto

\(P(A \cap B) = P(A) \cdot P(B \vert A)\) ou \(P(B \cap A) = P(B) \cdot P(A \vert B)\)

Ou seja, para que aconteça \(A \cap B\), é necessário impor que aconteça \(A\) e depois é necessário impor que conteça \(B\), dado que o eventyo \(A\) já tenha acontecido.

Generalização para 3 eventos

\[P(A \cap B \cap C) = P(B) \cdot P(B \vert A) \cdot P(C \vert A \cap B)\]

Eventos Independentes

Dois eventos são chamados independentes quando a probabilidde de acontecer um dado que aconteceu outro, é igual à probabilidade sem informação nenhuma. Ou seja:

\[P(A \vert B) = P(A)\]

Portanto, a informação sobre o evento \(B\) não altera a probabilidade de ocorrência de \(A\).

Teorema do Produto Simplificado

No caso especial de eventos independentes, o teorema do produto para dois eventos é:

\[P(A \cap B) = P(A) \cdot P(B)\]

Generealizando para K eventos:

\[P(A \cap B \cap ... \cap K) = P(A) \cdot P(B) \cdot ... \cdot P(K)\]