Aula 01

Probabilidade

Probabilidade é o estudo da aleatoriedade e da incerteza. É a quantificação sobre o conhecimento que temos de um determinado evento.

Experimentos

Existem dois tipos de experimentos:

• Determinísticos - Um evento em que os resultados podem ser previstos
• Aleatório - Um experimento em que os resultados são diferentes em cada vez que ele é repetido.

Espaço amostral

A relação de todos os resultados possíveis de um experimento é o espaço amostral. Representamos um espaço amostral, ou espaço amostral universal como também é chamado, pela letra \(S\).

No caso da moeda representamos o seu espaço amostral por:

\[S = \{ cara, coroa \}\]

Se novamente ao invés de uma moeda, o objeto a ser lançado for um dado, o espaço amostral será:

\[S = \{ 1, 2, 3, 4, 5, 6 \}\]

Eventos

Quando lançamos um dado ou uma moeda, chamamos a ocorrência deste fato de evento., Ou seja, um subconjunto do espaço amostral é um evento. Pode ser constituído por um ou mais resultados.

\[A = \{ 2, 3, 5 \}\]

Note que \(A \subset S\) (\(A\) está contido em \(S\), \(A\) é um subconjunto de \(S\)). O conjunto \(A\) é a representação do evento do lançamento de um dado, quando temos a face para cima igual a um número primo.

Classificação de Eventos

Para calcular a probabilidade de um evento ocorrer, antes de realizar o experimento, devemos angariar todas as informações que pudermos, sobre o evento, e calcular as probabilidades de cada evento elementar que compõe o evento complexo que se deseja conhecer. Para isso, usamos as operações entre eventos.

Evento Simples

Eventos simples são os eventos que são formados por um único elemento do espaço amostral.

\(A = \{ 5 \}\) é a representação de um evento simples do lançamento de um dado cuja face para cima é divisível por 5. Nenhuma das outras possibilidades são divisíveis por 5.

Evento Certo

Ao lançarmos um dado é certo que a face que ficará para cima, terá um número divisor de 720. Este é um evento certo, pois:

\(720 = 6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1\),

Obviamente qualquer um dos números da face de um dado é um divisor de 720, pois 720 é o produto de todos eles.

O conjunto \(A = \{ 2, 3, 5, 6, 4, 1 \}\) representa um evento certo pois ele possui todos os elementos do espaço amostral \(S = \{ 1, 2, 3, 4, 5, 6 \}\).

Evento Impossível

No lançamento conjunto de dois dados qual é a possibilidade de a soma dos números contidos nas duas faces para cima, ser igual a 15?

Este é um evento impossível, pois o valor máximo que podemos obter é igual a doze. Podemos representá-lo por , ou ainda por \(A = \{\}\).

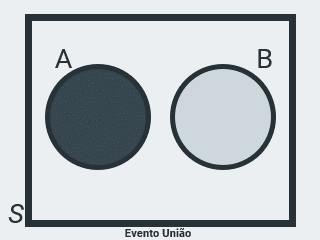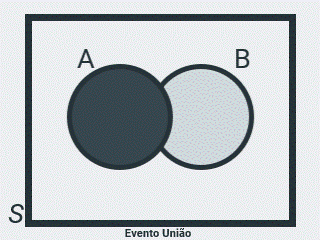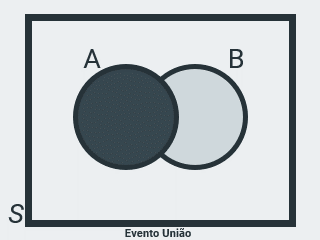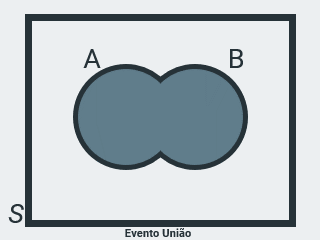
Evento União

Seja \(A = \{ 1, 3 \}\) o evento de ocorrência da face superior no lançamento de um dado, ímpar e menor ou igual a 3 e \(B = \{ 3, 5 \}\), o evento de ocorrência da face superior, ímpar e maior ou igual a 3, então \(C = \{ 1, 3, 5 \}\) representa o evento de ocorrência da face superior ímpar, que é a união dos conjuntos A e B, ou seja, a operação \(A \cup B\) acontece quando acontecer ou o evento \(A\), ou o evento \(B\), ou os dois (quando ocorrer algum um dos eventos).

Note que o evento C contém todos os elementos de A e B.

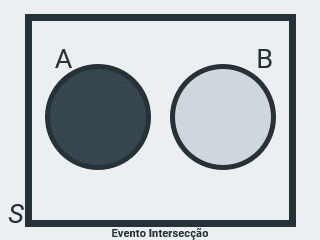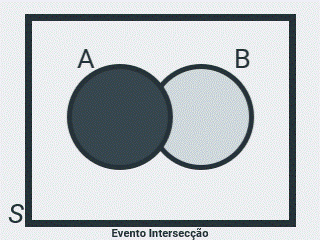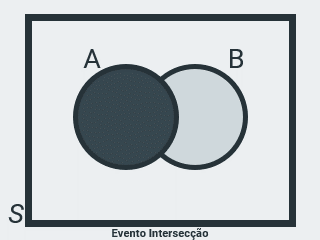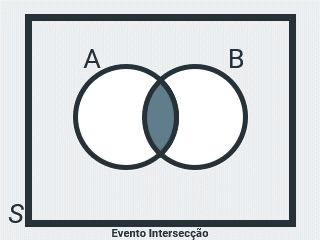
Evento Intersecção

Seja \(A = \{ 2, 4 \}\) o evento de ocorrência da face superior no lançamento de um dado, par e menor ou igual a 4 e \(B = \{ 4, 6 \}\), o evento de ocorrência da face superior, par e maior ou igual a 4, então \(C = \{ 4 \}\) representa o evento de ocorrência da face superior par, que é a intersecção dos conjuntos A e B, ou seja, a operação \(A \cap B\) acontece quando ocorre o evento \(A\) E o evento \(B\). Ou seja, quando ocorrem os dois eventos.

Veja que o evento C contém apenas os elementos comuns a A e B.

Complementar

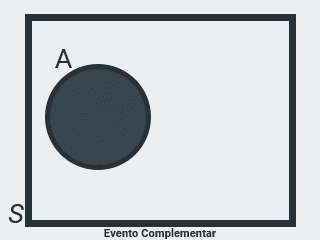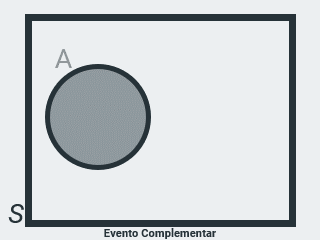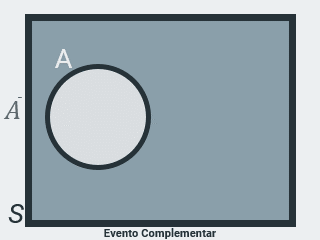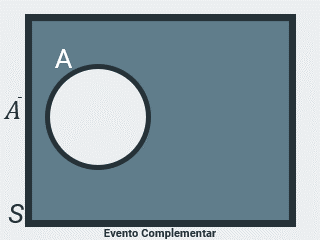
Seja \(A = \{ 1, 3, 5 \}\) o evento de ocorrência da face superior no lançamento de um dado, um número ímpar, o seu evento complementar é \(\bar A = \{ 2, 4, 6 \}\) o evento de ocorrência da face superior no lançamento de um dado, um número par.

Os elementos de \(\bar A\) são todos os elementos do espaço amostral \(S\) que não estão contidos em \(A\) (não pertencem ao evento considerado), então temos que \(\bar A = S - A\) e ainda que \(S = A + \bar A\). ou seja, o evento complementar significa a não ocorrência do evento considerado.

Eventos mutuamente excludentes

Seja \(A = \{ 1, 2, 3, 6 \}\) o evento de ocorrência da face superior no lançamento de um dado, um número divisor de 6 e \(B = \{ 5 \}\), o evento de ocorrência da face superior, um divisor de 5, os eventos A e B são mutuamente exclusivos, pois , isto é, os eventos não possuem elementos em comum.

Quando dois eventos \(A\) e \(B\) (\(A \cap B = \varnothing\)) não possuírem nenhum resultado em comum, significa que esses eventos são mutualmente exclusivos. OU seja: quando um acontece, o outro não pode acontecer.